X線作業主任者の過去問の解説：管理（2014年10月）

ここでは、2014年（平成26年）10月公表の過去問のうち「エックス線の管理に関する知識（問1～問10）」について解説いたします。

それぞれの科目の解説は、下記ページからどうぞ。

◆X線作業主任者の過去問の解説：管理（2014年10月）
◆X線作業主任者の過去問の解説：法令（2014年10月）
◆X線作業主任者の過去問の解説：測定（2014年10月）
◆X線作業主任者の過去問の解説：生体（2014年10月）

問1 エックス線に関する次の記述のうち、誤っているものはどれか。

（1）エックス線は、荷電粒子の流れである。
（2）エックス線は、間接電離放射線である。
（3）連続エックス線は、制動放射により発生する。
（4）特性エックス線は、軌道電子がエネルギー準位の高い軌道から低い軌道へと転移するとき発生する。
（5）特性エックス線は、線スペクトルを示す。

問2　工業用エックス線装置のエックス線管及びエックス線の発生に関する次の記述のうち、誤っているものはどれか。

（1）陰極のフィラメントには、通常、融点が高いタングステンが用いられる。
（2）陰極のフィラメント端子間の電圧は、フィラメント加熱用の降圧変圧器を用いて10～20 V程度にされている。
（3）陰極のフィラメントが白熱状態に加熱されることによりフィラメント金属中の自由電子がエネルギーを得て、金属表面から飛び出したものを熱電子という。
（4）陰極には、発生した熱電子のひろがりをおさえるための集束カップ（集束筒）が設けられている。
（5）陽極のターゲットはエックス線管の軸に対して斜めになっており、加速された熱電子が衝突しエックス線が発生する領域である実焦点よりも、これをエックス線束の利用方向から見た実効焦点の方が大きくなるようにしてある。

問3　工業用の分離形エックス線装置に関する次の文中の［　　］に入れるAからCの語句の組合せとして、正しいものは（1）～（5）のうちどれか。
「工業用の分離形エックス線装置は、エックス線管、［　A　］、高電圧発生器、［　B　］、［　C　］で構成される装置である。」

（1）［A］エックス線制御器　　［B］管電流調整器　　　［C］高電圧ケーブル
（2）［A］エックス線制御器　　［B］管電圧調整器　　　［C］低電圧ケーブル
（3）［A］管電圧調整器　　　　［B］管電流調整器　　　［C］高電圧ケーブル及び低電圧ケーブル
（4）［A］エックス線管冷却器　［B］管電圧調整器　　　［C］高電圧ケーブル
（5）［A］エックス線管冷却器　［B］エックス線制御器　［C］高電圧ケーブル及び低電圧ケーブル

問4　エックス線の減弱に関する次の文中の［　　］内に入れるAからCの式及び語句の組合せとして、正しいものは（1）～（5）のうちどれか。

「単一エネルギーのエックス線の細い平行線束が厚さxの吸収体に垂直に入射する場合、入射したエックス線の強度をI₀、透過した直後のエックス線の強度をI、［　A　］をμとすれば、Iは次式によって表される。
　I = I₀exp(-μx)
線束が太いときには、ビルドアップ（再生）係数Bを用いて、［　B　］式によって表される。この式において、Bは1より［　C　］。」

（1）［A］質量減弱係数　［B］I = I₀exp(-Bμx)　［C］小さい
（2）［A］線減弱係数　　［B］I = I₀exp(-Bμx)　［C］大きい
（3）［A］質量減弱係数　［B］I = I₀exp(-μx/B) ［C］小さい
（4）［A］線減弱係数　　［B］I = BI₀exp(-μx)　［C］大きい
（5）［A］質量減弱係数　［B］I = BI₀exp(-μx)　［C］小さい

問5　連続エックス線が物体を透過する場合の減弱に関する次の記述のうち、正しいものはどれか。

（1）連続エックス線が物体を透過するとき、平均減弱係数は、物体の厚さの増加に伴い大きくなる。
（2）連続エックス線が物体を透過すると、最高強度を示すエックス線エネルギーは、低い方へ移動する。
（3）連続エックス線が物体を透過するとき、透過後の実効エネルギーは物体の厚さが増すほど高くなるが、物体が十分厚くなるとほぼ一定となる。
（4）連続エックス線は、物体を透過しても、その全強度は変わらない。
（5）連続エックス線が物体を透過するとき、透過エックス線の全強度が物体に入射する直前の全強度の1/2になる物体の厚さをH_aとし、直前の全強度の1/4になる物体の厚さをH_bとすれば、H_bはH_aの2倍に等しい。

問6　エックス線を鋼板に照射したときの散乱線に関する次の記述のうち、誤っているものはどれか。
ただし、特に記述したもの以外の散乱に関する条件はすべて同一とする。

（1）前方散乱線の空気カーマ率は、散乱角が大きくなるに従って減少する。
（2）前方散乱線の空気カーマ率は、鋼板の板厚が増すに従って減少する。
（3）後方散乱線の空気カーマ率は、管電圧が高くなるに従って増加する。
（4）後方散乱線の空気カーマ率は、エックス線装置の影になるような位置を除き、散乱角が大きくなるに従って増加する。
（5）後方散乱線の空気カーマ率は、鋼板の板厚が増すに従って減少する。

問7　エックス線の遮へい及び散乱線の低減方法等に関する次の記述のうち、誤っているものはどれか。

（1）ろ過板として、管電圧120～300 kVのエックス線装置にはアルミニウムを用い、管電圧120 kV以下のエックス線装置には銅を用いる。
（2）絞りは、エックス線束の広がりを制限し、エックス線を必要な部分にだけ照射するために用いる。
（3）遮へい体としては、原子番号が大きく、密度の高い物質を用いるのがよい。
（4）鉛板、鋼板、コンクリートのうち、同一の厚さでの遮へい効果は、鉛板が最も大きい。
（5）照射筒は、放射ロに取付けるラッパ状の遮へい体で、エックス線束及び散乱線が外部へ漏えいしないようにするために用いる。

問8　エックス線装置を使用する事業場における管理区域を設定するための外部放射線の測定に関する次の記述のうち、誤っているものはどれか。

（1）測定器は、シンチレーション式サーベイメータを用いることとし、積算型放射線測定器を用いてはならない。
（2）位置により線量率の変化が大きいと予測される場合には、測定点を密にとる。
（3）あらかじめバックグラウンド値を調査しておき、これを測定器の指示値から差し引いた値を測定結果とする。
（4）測定は、あらかじめ計算により求めた1 cm線量当量又は1 cm線量当量率の低い箇所から逐次高い箇所へと行っていく。
（5）測定点の高さは、作業床面上約1 mの位置とする。

問9　あるエックス線装置のエックス線管の焦点から1 m離れた点での1 cm線量当量率は120 mSv/hであった。
このエックス線装置を用いて、鉄板とアルミニウム板を重ね合わせた板に細い線束のエックス線を照射したとき、エックス線管の焦点から1 m離れた点における透過後の1 cm線量当量率は30 mSv/hであった。
このとき、鉄板とアルミニウム板の厚さの組合せとして正しいものは次のうちどれか。
ただし、このエックス線の鉄に対する減弱係数を3.0 cm^-1、アルミニウムに対する減弱係数を0.5 cm^-1とし、鉄板及びアルミニウム板を透過した後のエックス線の実効エネルギーは、透過前と変わらないものとする。
また、散乱線による影響は無いものとする。
なお、log_e2＝0.69とする。

［A］＝鉄板、［B］＝アルミニウム板
（1）［A］2.3 mm　［B］13.8 mm
（2）［A］2.3 mm　［B］20.7 mm
（3）［A］3.5 mm　［B］27.6 mm
（4）［A］4.6 mm　［B］13.8 mm
（5）［A］4.6 mm　［B］20.7 mm

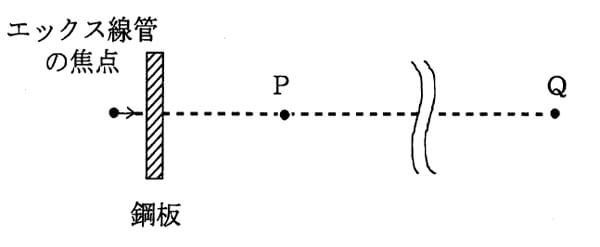
問10　下図のように、エックス線装置を用いて鋼板の透過写真撮影を行うとき、エックス線管の焦点から5 mの距離のP点における写真撮影中の1 cm線量当量率は0.5 mSv/hである。
露出時間が1枚につき90秒の写真を週90枚撮影するとき、焦点から管理区域の境界線上のQ点までの距離に最も近い値は（1）～（5）のうちどれか。
ただし、3か月は13週とする。

（1）11 m
（2）13 m
（3）15 m
（4）17 m
（5）19 m

Tweet