X線作業主任者の過去問の解説：管理（2019年10月）

ここでは、2019年（令和元年）10月公表の過去問のうち「エックス線の管理に関する知識（問1～問10）」について解説いたします。

それぞれの科目の解説は、下記ページからどうぞ。

◆X線作業主任者の過去問の解説：管理（2019年10月）
◆X線作業主任者の過去問の解説：法令（2019年10月）
◆X線作業主任者の過去問の解説：測定（2019年10月）
◆X線作業主任者の過去問の解説：生体（2019年10月）

問1　エックス線管及びエックス線の発生に関する次の記述のうち、誤っているものはどれか。

（1）エックス線管の内部は、効率的にエックス線を発生させるため、高度の真空になっている。
（2）陰極で発生する熱電子の数は、フィラメント電流を変えることで制御される。
（3）陽極のターゲットは、エックス線管の軸に対して斜めになっており、加速された熱電子が衝突しエックス線が発生する領域である実焦点よりも、これをエックス線束の利用方向から見た実効焦点の方が大きくなるようにしてある。
（4）連続エックス線の発生効率は、ターゲット元素の原子番号と管電圧の積に比例する。
（5）管電圧がターゲット元素に固有の励起電圧を超える場合、発生するエックス線は、制動放射による連続エックス線と線スペクトルを示す特性エックス線が混在したものになる。

問2　エックス線管の管電流又は管電圧の変化に対応したエックス線の発生に関する次の記述のうち、誤っているものはどれか。

（1）管電圧を一定にして管電流を上げると、エックス線の全強度は、管電流に比例して増加する。
（2）管電流を一定にして管電圧を上げると、エックス線の全強度は、管電圧に比例して増加する。
（3）管電圧を一定にして管電流を上げても、エックス線の最大エネルギーは変わらない。
（4）管電流を一定にして管電圧を上げると、エックス線の最大エネルギーは高くなる。
（5）管電流を一定にして管電圧を上げると、エックス線の最短波長は、管電圧に反比例して短くなる。

問3　特性エックス線に関する次の記述のうち、正しいものはどれか。

（1）特性エックス線の波長は、ターゲット元素の原子番号が大きいほど長くなる。
（2）特性エックス線は、連続スペクトルを示す。
（3）管電圧が、K系列の特性エックス線を発生させるのに必要な限界値であるK励起電圧を下回るときは、他の系列の特性エックス線も発生することはない。
（4）K殻電子が電離されたことにより特性エックス線が発生することをオージェ効果という。
（5）K系列の特性エックス線は、管電圧を上げると強度が増大するが、その波長は変わらない。

問4　エックス線と物質との相互作用に関する次の記述のうち、誤っているものはどれか。

（1）入射エックス線のエネルギーが中性子1個の静止質量に相当するエネルギー以上になると、電子及び陽電子を生じる電子対生成が起こるようになる。
（2）コンプトン効果とは、エックス線光子と原子の軌道電子とが衝突し、電子が原子の外に飛び出し、光子が運動の方向を変える現象である。
（3）コンプトン効果による散乱エックス線は、入射エックス線のエネルギーが高くなるほど前方に散乱されやすくなる。
（4）光電効果とは、原子の軌道電子がエックス線光子のエネルギーを吸収して原子の外に飛び出し、光子が消滅する現象である。
（5）光電効果が生じる確率は、入射エックス線のエネルギーが増大すると、コンプトン効果に比べて急激に低下する。

問5　あるエックス線装置のエックス線管の焦点から1m離れた点での1cm線量当量率は120mSv/hであった。
このエックス線装置を用いて、鉄板とアルミニウム板を重ね合わせた板に細い線束のエックス線を照射したとき、エックス線管の焦点から1m離れた点における透過後の1cm線量当量率は7.5mSv/hであった。
このとき、鉄板とアルミニウム板の厚さの組合せとして正しいものは次のうちどれか。
ただし、このエックス線に対する鉄の減弱係数を3.0cm^－1、アルミニウムの減弱係数を0.5cm^－1とし、鉄板及びアルミニウム板を透過した後のエックス線の実効エネルギーは、透過前と変わらないものとする。
また、散乱線による影響は無いものとする。
なお、 log_e2＝0.69とする。

［A］＝鉄板　［B］＝アルミニウム板
（1）［A］2.3mm　［B］20.7mm
（2）［A］2.3mm　［B］27.6mm
（3）［A］4.6mm　［B］20.7mm
（4）［A］4.6mm　［B］27.6mm
（5）［A］6.9mm　［B］20.7mm

問6　単一エネルギーの細いエックス線束が物体を透過するときの減弱に関する次の記述のうち、正しいものはどれか。

（1）半価層の値は、エックス線の線量率が高いほど大きくなる。
（2）半価層の値は、1MeV程度以下のエネルギー範囲では、エックス線のエネルギーが高いほど小さくなる。
（3）半価層h（cm）と減弱係数μ（cm^－1）との間には、μh＝log₁₀2の関係がある。
（4）硬エックス線の半価層の値は、軟エックス線の半価層の値より大きい。
（5）半価層の5倍に相当する厚さが、1/10価層である。

問7　エックス線の散乱に関する次の文中の［　　］内に入れるAからCの語句又は数値の組合せとして、正しいものは（1）～（5）のうちどれか。

「エックス線装置を用い、管電圧100kVで、厚さが20mmの鋼板及びアルミニウム板のそれぞれにエックス線のビームを垂直に照射し、散乱角135°方向の後方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定してその大きさを比較したところ、［　A　］の後方散乱線の方が大きかった。
次に、同じ照射条件で、鋼板について、散乱角120°及び135°の方向の後方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、［　B　］方向の方が大きかった。
また、同じ照射条件で、鋼板について、散乱角30°及び60°の方向の前方散乱線の空気カーマ率を、照射野の中心から2mの位置で測定し、その大きさを比較したところ、［　C　］方向の方が大きかった。」

（1）［A］鋼板　［B］120°　［C］60°
（2）［A］鋼板　［B］135°　［C］30°
（3）［A］鋼板　［B］135°　［C］60°
（4）［A］アルミニウム板　［B］120°　［C］60°
（5）［A］アルミニウム板　［B］135°　［C］30°

問8　ろ過板に関する次の文中の［　　］内に入れるAからCの語句の組合せとして、正しいものは（1）～（5）のうちどれか。

「ろ過板は、照射口に取り付けて、透過試験に役立たない［　A　］エックス線（波長の［　B　］エックス線）を取り除き、無用な散乱線を減少させるために使用する。
しかし、［　C　］などで［　A　］エックス線そのものを利用する場合には、ろ過板は使用しない。」

（1）［A］硬　［B］長い　［C］エックス線回折装置
（2）［A］硬　［B］短い　［C］蛍光エックス線分析装置
（3）［A］硬　［B］短い　［C］エックス線回折装置
（4）［A］軟　［B］長い　［C］蛍光エックス線分析装置
（5）［A］軟　［B］短い　［C］エックス線CT装置

問9　エックス線装置を使用する管理区域を設定するための外部放射線の測定に関する次の記述のうち、誤っているものはどれか。

（1）放射線測定器は、方向依存性が少ないものを使用する。
（2）測定は、1cm線量当量及び70μm線量当量について行う。
（3）位置によって測定値の変化が大きいと予測される場合は、測定点を密にとる。
（4）測定者は、外部放射線の測定中には必ず放射線測定器を装着する。
（5）測定箇所については、壁などの構造物によって区切られた境界の近辺の箇所を含むようにする。

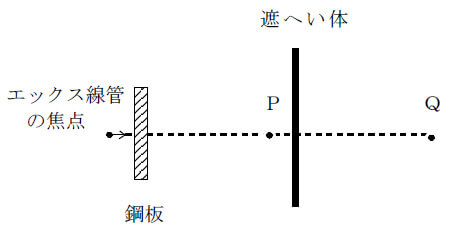
問10　下図のようにエックス線装置を用いて鋼板の透過写真撮影を行うとき、エックス線管の焦点から4mの距離にあるP点における写真撮影中の1cm線量当量率は、160μSv/hである。
この装置を使って、露出時間が1枚につき2分の写真を週300枚撮影するとき、P点の後方に遮へい体を設けることにより、エックス線管の焦点からP点の方向に8mの距離にあるQ点が管理区域の境界線上にあるようにすることのできる遮へい体の厚さは、次のうちどれか。
ただし、遮へい体の半価層は10mmとし、3か月は13週とする。

（1）10mm
（2）15mm
（3）20mm
（4）25mm
（5）30mm

Tweet